W15 <<
Previous 影片整理
影片1
首先要先找出A1以及A2的夾角,可以透過畢氏定理列出
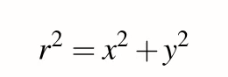
並透過餘弦定理可以將公式轉換為
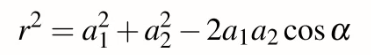
將公式用COSalpha表示,並將r2次方帶入第一個公式得
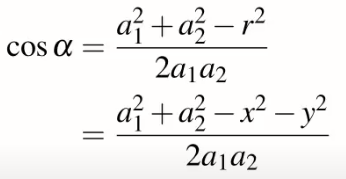
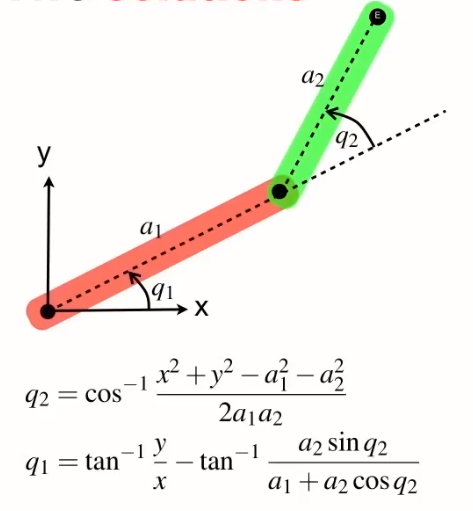
再透過下圖我們可以得知q2=180-alpha
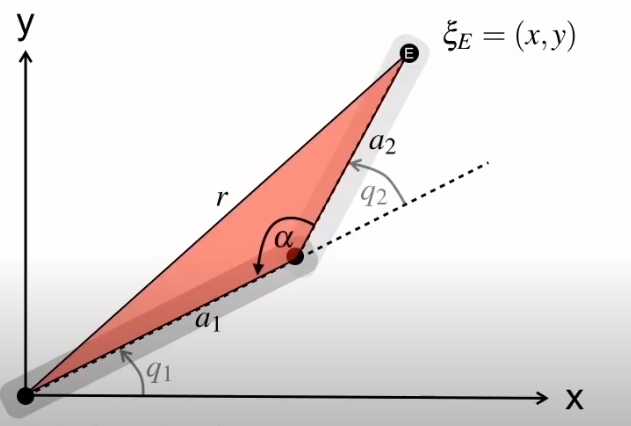
因此可得知COSq2=-COSalpha,將負號移過去可以得到
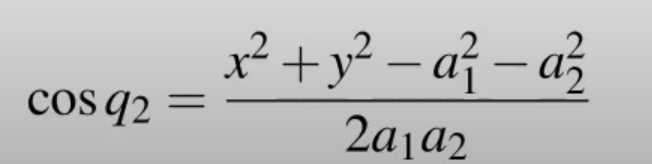
因此我們可以得知q2
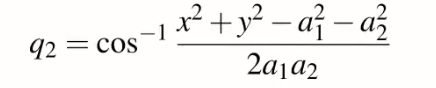
接下來,以a2為長邊畫出一個直角三角形
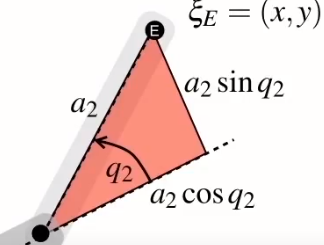
由這個三角形我們可以得到
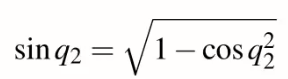
此時劃出一個連接兩條手臂的直角三角形
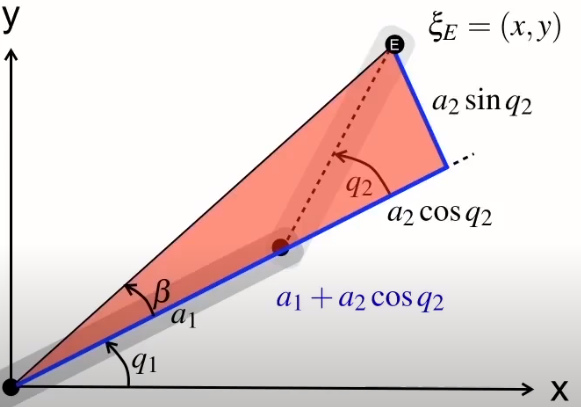
透過此三角形可得出beta角公式
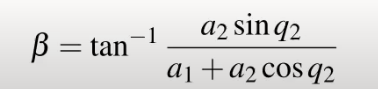
劃出一個大直角三角形
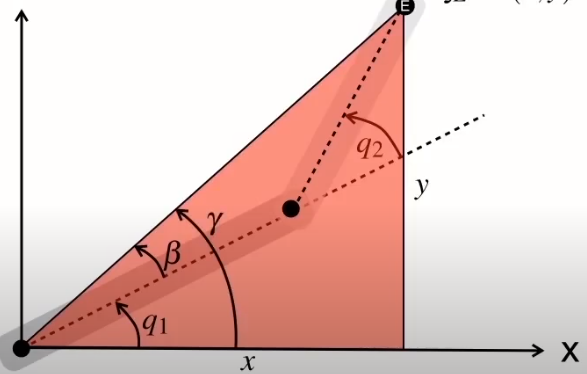
由此三角形可推得
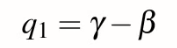
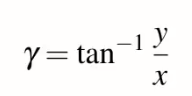
透過前面所推導的公式q1可得
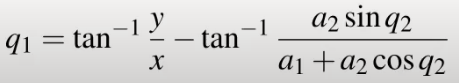
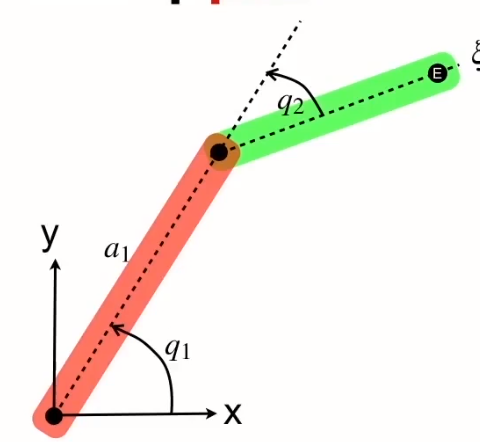
若手臂移動,如下圖
因alpha、beta以及q1關系改變
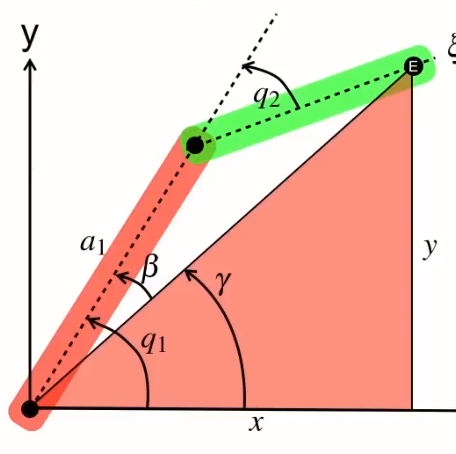
則q1和q2公式會變為
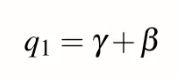
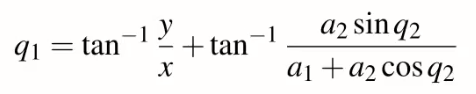
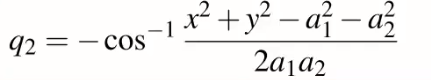
此為兩種比較圖
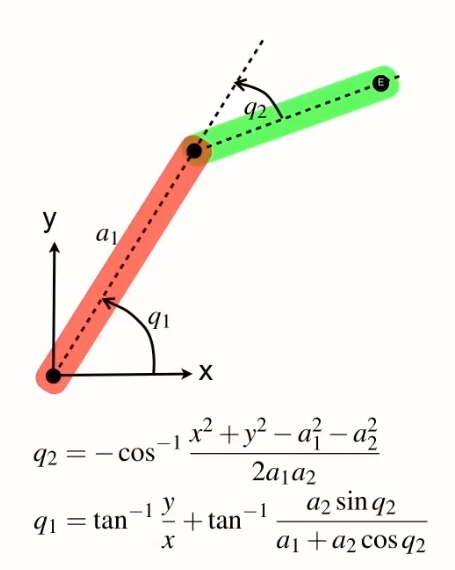

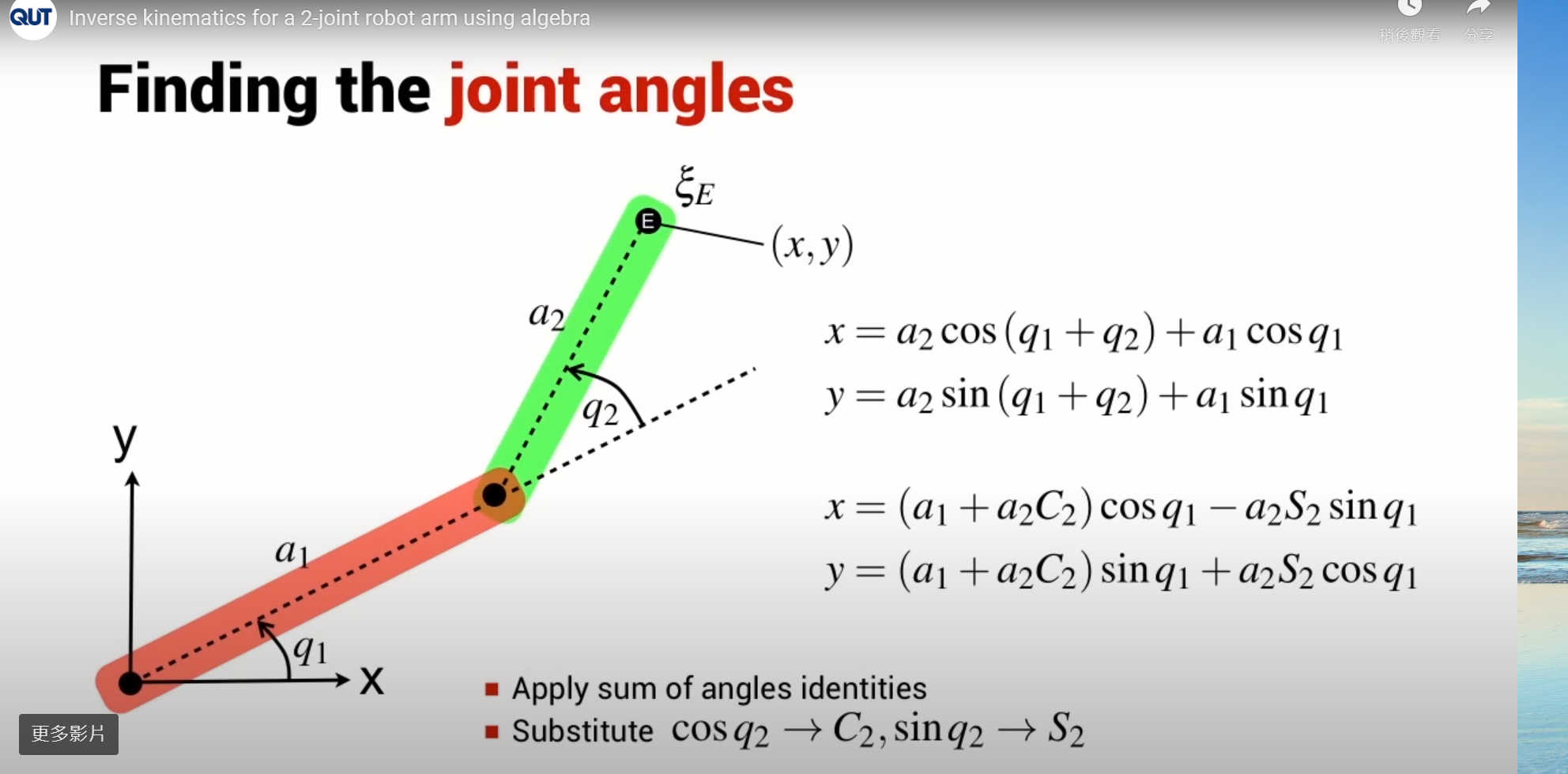
特定的線性函數不是幾何,有一個表達式E
旋轉q1沿x方向平移a1;旋轉q2,由a2在x方向進行平移,如果展開這個,全部相乘
一起轉變得到此表達式,表示尾端姿態的矩陣
分解x與y座標
平方X和Y方程式後兩兩相加可得知角度q2
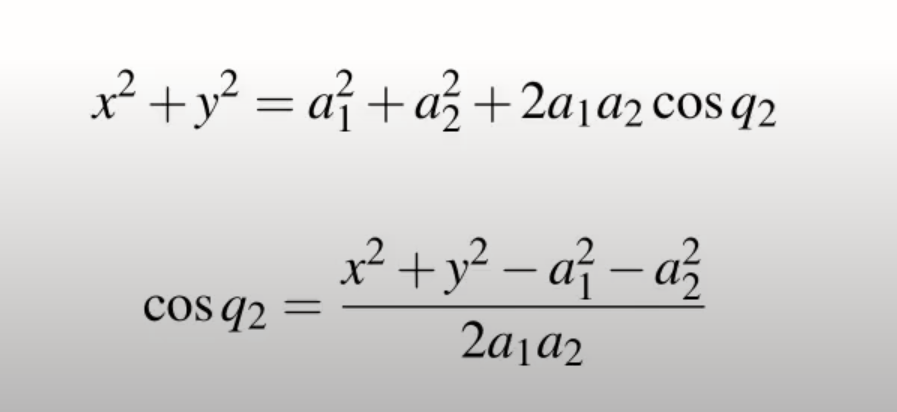
製作後的方程式:
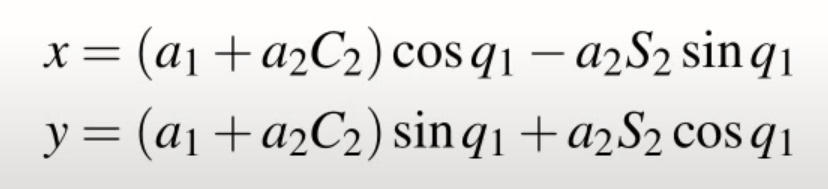
此為已知方程式:

只考慮y的方程式,可以確定a、b、c值,一旦知道這些,那麼就可以有q1的方程式
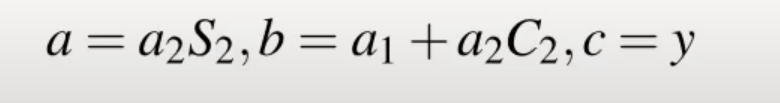
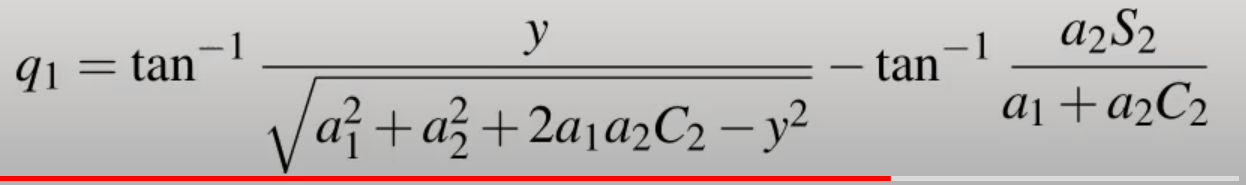
將前面得知地此式,帶入q1進行簡化
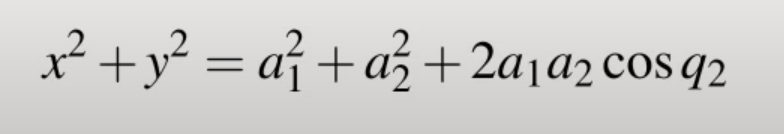
即可得此式
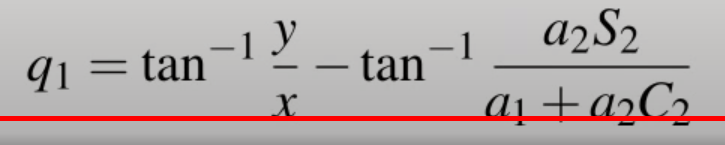
======= >>>>>>> 1adb32d0ef62bdf1b9851bfb00b5ec8ef2b5cd72
W15 <<
Previous